Let's start with loading libraries and files,
> library('corrgram')
> library(easyGgplot2)
> library('forcats')
> library(neuralnet)
> library(ggplot2)
> library(dplyr)
> library(randomForest)
> train <- read_csv('train.csv')
> test <- read_csv('test.csv')
> test$Survived <- NA
> combine <- rbind(train,test)
Let's check NA's.
> apply(combine, 2, function(x) sum(is.na(x)))
PassengerId Survived Pclass Name
0 418 0 0
Sex Age SibSp Parch
0 263 0 0
Ticket Fare Cabin Embarked
0 1 1014 2
> glimpse(combine)
Observations: 1,309
Variables: 12
$ PassengerId <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 1...
$ Survived <int> 0, 1, 1, 1, 0, 0, 0, 0, 1, 1...
$ Pclass <int> 3, 1, 3, 1, 3, 3, 1, 3, 3, 2...
$ Name <chr> "Braund, Mr. Owen Harris", "...
$ Sex <chr> "male", "female", "female", ...
$ Age <dbl> 22, 38, 26, 35, 35, NA, 54, ...
$ SibSp <int> 1, 1, 0, 1, 0, 0, 0, 3, 0, 1...
$ Parch <int> 0, 0, 0, 0, 0, 0, 0, 1, 2, 0...
$ Ticket <chr> "A/5 21171", "PC 17599", "ST...
$ Fare <dbl> 7.2500, 71.2833, 7.9250, 53....
$ Cabin <chr> NA, "C85", NA, "C123", NA, N...
$ Embarked <chr> "S", "C", "S", "S", "S", "Q"...
Pclass is the passenger class which is 1,2 or 3. SibSp is the number of siblings or spouses travelling together. Parch is the number of parents or children travelling together. Ticket is the ticket number and the embarked is the port of embarkation.
Now we are converting Survived, Pclass, Embarked and Sex to factor and reconstruct combine data frame.
> train <- train %>% mutate(Survived = factor(Survived),
Pclass=factor(Pclass),Embarked=factor(Embarked),Sex = factor(Sex))
> test <- test %>% mutate(Pclass=factor(Pclass),Embarked=factor(Embarked),Sex = factor(Sex))
> combine <- rbind(train,test)
How many of passengers are survived from the accident?
> train %>% count(Survived)
# A tibble: 2 × 2
Survived n
<fctr> <int>
1 0 549
2 1 342
> p1 <- ggplot(train, aes(x=Pclass,fill=Survived)) + geom_bar(position='fill')
> p2 <- ggplot(train,aes(x=Age,color=Survived)) + geom_freqpoly(binwidth=1) + theme(legend.position = "none")
> p3 <- ggplot(train,aes(x=Age,color=Survived)) + geom_density() + theme(legend.position = "none")
> p4 <- ggplot(train,aes(x = SibSp+Parch,fill=Survived)) + geom_bar(position='fill') + theme(legend.position = "none")
> p5 <- ggplot(train,aes(x = Fare, color = Survived)) + geom_freqpoly(binwidth=0.04) + scale_x_log10() + theme(legend.position = "none")
> ggplot2.multiplot(p1,p2,p3,p4,p5)
Obviously survive rate is higher as the Pclass goes towards 1. For Age, we have multiple plots. One is frequency the other is density plot. The most notable pattern in those plots is the survival rate among passengers who are under 10 years old. For SibSp + Parch, which can be thought as family size is also correlated with survival. Looks like small families with SibSp + Parch less than 4 have better chance to survive. Fare has very wide range, even with the logaritmic values. Fare plot shows that when Fare goes up survival chances are also go up.
Let's see how the features are correlated among each other. In order to create a correlation matrix
all features must be numeric. We don't need PassengerId, Name, Cabin and Ticket.
> pCor <- train[,-c(1,4,9,11)] %>% mutate(Sex = fct_recode(Sex,"0" = "male",
"1" = "female") ) %>%
mutate(Sex = as.integer(Sex),
Pclass = as.integer(Pclass),
Survived = as.integer(Survived),
Embarked = as.integer(Embarked))
> corrgram(pCor,lower.panel=panel.pie,main = "Correlation Among Features")
As seen in previous plots, Sex, Pclass and Fare are more correlated with Survived than other features. Also there is a certain amount of correlation between Fare and Pclass, another correlation is between Pclass and Age. Elderly people have chosen better classes? Maybe.
1. Handling With Missing Cells
> apply(combine,2,function(x) sum(is.na(x)) )
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket
0 418 0 0 0 263 0 0 0
Fare Cabin Embarked
1 1014 2
1.1 Age
How can we deal with age? There are 263 missing values, which is considerably high. There is something that we can use in the data set. All names have some titles like Mr, Master, Miss etc. We can explore ages using those title since person who has title 'Master' is at most 8 years old. We can simply take the median of each title group and set it to missing cells. One can argue that it may cause overfitting. It is worth to work on it.
Let's find the titles using regular expressions.
> Title <- sub(".*,.([^.]*)\\..*","\\1",combine$Name)
> combine <- combine %>% mutate(Title = factor(Title)) %>%
mutate(Title = fct_collapse(Title, "Miss" = c("Mlle", "Ms"), "Mrs" = "Mme",
"Ranked" = c( "Major", "Dr", "Capt", "Col", "Rev"),
"Royalty" = c("Lady", "Dona", "the Countess", "Don", "Sir", "Jonkheer")))
> levels(combine$Title)
[1] "Ranked" "Royalty" "Master" "Miss" "Mrs" "Mr"
Let's see the survival rate of Title owners on train data set.
> train$Title <- combine$Title[1:891]
> p6 <- ggplot(train,aes(x=Title,fill = Survived)) + geom_bar(position="fill")
> p6
This plot also shows that females have higher chance to survive than males. Survival rate in Ranked is low, we can say that personal of the Titanic are mostly died. We will use Title feature to fill missing values on Age. Since Title feature highly supports Sex feature, including both may cause overfitting.
> combine <- combine %>% group_by(Title) %>% mutate(Age = ifelse(is.na(Age),round(median(Age, na.rm=T),1),Age))
We are done with Age. Next step will be Cabin. Cabin has 1014 NA values. Instead of filling it, let's look at survival rates on whether we know the cabin or not.
1.2 Cabin
> combine$cabinKnown <- ifelse(is.na(combine$Cabin),FALSE,TRUE)
> p7 <- ggplot(combine[1:891,], aes(x=cabinKnown,fill=Survived)) + geom_bar(position="fill")
WOW! Seems like survival rate is quite high if cabin is known. I wonder the what proportion of cabins are known per Pclass.
> p8 <- ggplot(train, aes(x=cabinKnown,fill=Survived)) + geom_bar() + facet_grid(~Pclass)
As suspected! If you are from first class they value your information more! And for sure, you have better chances to survive. I also want to know the relationship between Pclass, cabin number and Fare. Before that, we need to fill the empty cells on Fare and Cabin.
1.3 Fare
For fare, there is only one empty cell. Let's find that person.
> combine %>% filter(is.na(Fare))
Source: local data frame [1 x 14]
Groups: Title [1]
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
<int> <fctr> <fctr> <fctr> <fctr> <dbl> <int> <int> <fctr> <dbl> <fctr> <fctr>
1 1044 NA 3 Storey, Mr. Thomas male 60.5 0 0 3701 NA NA S
# ... with 2 more variables: Title <fctr>, cabinKnown <lgl>
He is a third class passenger who is 60.5 years old. The way we are going to fill empty fare cell is
following. Each passenger class (Pclass) has some certain fare values. Let's visualize it first.
> p9 <- ggplot(combine,aes(x=Pclass,y=Fare,color=Pclass)) + geom_boxplot() + scale_y_log10() + ggtitle('Fare v Pclass')
Here we can see that Fare in class one is distinctly higher that 2 and 3. Similarly there is a considerably high difference between class 2 and 3. Class 3 has some outliers. We will fill the NA by taking the median of Fare's in class 3.
>Fare=ifelse(is.na(combine$Fare)&combine$Pclass==3,round(median(na.omit(combine$Fare)),1),combine$Fare)
> combine$Fare = Fare
Great! Now let's look at the 2 missing cells in Embarked.
1.4 Embarked
> combine%>%filter(is.na(Embarked))
Source: local data frame [2 x 15]
Groups: Fare [1]
PassengerId Survived Pclass Name Sex Age SibSp Parch Ticket
<int> <fctr> <fctr> <fctr> <fctr> <dbl> <int> <int> <fctr>
1 62 1 1 Icard, Miss. Amelie female 38 0 0 113572
2 830 1 1 Stone, Mrs. George Nelson (Martha Evelyn) female 62 0 0 113572
# ... with 6 more variables: Fare <dbl>, Cabin <fctr>, Embarked <fctr>, Title <fctr>, cabinKnown <lgl>,
# fareFull <dbl>
They are first class female passengers. And their Ticket number is the same! They should have embarked from the same point. These two ladies make us curious about shared tickets since they have the same ticket!
> p10 <- ggplot(combine, aes(x=Embarked,y=Pclass)) + geom_jitter(colour=combine$Pclass)
Plot shows that first class passengers are embarked mostly from C and S. The probability that a given
first class passenger has embarked from point C is higher than point S. We can see it by looking to intensity of the other class' passengers. By the way S is Southampton, C is Cherbourg and Q is Queenstown as written in wikipedia. From Southampton, high amount of passengers have embarked, but those passengers are mostly third class passengers. For this reason we decide to fill empty cells as Cherbourg, C.
> combine <- combine %>% mutate(Embarked = as.character(Embarked)) %>% mutate(Embarked = ifelse(is.na(Embarked),'C',Embarked)) %>% mutate(Embarked = as.factor(Embarked))
Great! Now let's look into the not-so-secret groups among passengers. We are going to look at ticket groups, families and children.
2. Feature Engineering via Groups
There are certain types of groups among passengers that have better/worse chances to survive. These are may include ticket groups, family size, being children and being alone.
2.1 Ticket Group and Family
> ticketGroup <- combine %>% group_by(Ticket) %>% summarise(count=n())
> familySize <- combine$SibSp + combine$Parch
What do you think about the probability of shared tickets are actually shared by families? Let's find the correlation between these two vectors and see it.
> cor(combine$count,familySize)
[1] 0.8005555
Looks like they are highly correlated. For this reason we will contine with only count, which is the number of people who share the same ticket.
> ticketGroup <- ticketGroup %>% mutate(count = as.character(count)) %>% mutate(count = as.factor(count))
> combine <- left_join(combine,ticketGroup,by="Ticket")
> p11 <- ggplot(combine[1:891,],aes(x=count,fill=Survived)) + geom_bar(position='fill')
This plot gives us a clue about the advantage of being among of small groups. If you are sharing your ticket with a person or two or three, you have better chances to survive.
Let's look at the family size versus survival rate.
> p12 <- ggplot(combine[1:891,],aes(Parch,SibSp,color=Survived)) + geom_count()
> combine$large_family <- (combine$Parch > 3) | (combine$SibSp > 2)
> ggplot(combine[1:891,],aes(x=large_family,fill=Survived)) + geom_bar(position="fill")
Being member of a large family decreases the odds of survival.
2.2 Fare
Fare feature involves ticket's fare. People who are shared their ticket should also be shared the price
if it.
> combine$fareShared = combine$Fare / as.numeric(as.character(combine$count))
2.3 Children
In the density plot above we showed that children have better chances to survive. So let's create another feature which is being children.
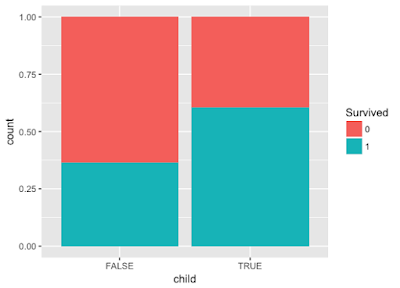
> combine$child <- combine$Age < 10
> p13 <- ggplot(combine[1:891,],aes(x=child,fill=Survived)) + geom_bar(position='fill')
Here we can see that passengers who are below 10 have better chances to survive.
2.4 No Family Member on Board - Alone
Now let's find the passengers that don't belong to any family group.
> combine <- combine %>% mutate(alone=(SibSp==0)&(Parch==0))
> p14 <- ggplot(combine[1:891,],aes(x=alone,fill=Survived)) + geom_bar(position = 'fill')
We can see that passengers who are alone have less chances to survive than who are not.
3. Model
Even if there are still a lot of room for improvement for features, let's stop there and take a look at
how our features will perform. We will construct a prediction model using bagging. Bagging is a method to decrease variance of a statistical learning method. Here we are going to use it with decision trees. Decision trees are suffered from high variance. bagging allows us to separate different prediction models using each training set and average them. Further information can be found here. The advantage we are going to get from using decision tree, that is random forest is that it gives us a importance values of each feature so that we can see our features roles on predicting the Survived passengers.
> train <- combine[1:891,c(2,3,5,6,12,14,17,19,20,21)]
> test <- combine[892:1309,c(3,5,6,12,14,17,19,20,21)]
> rf <-randomForest(Survived~Pclass+Sex+Embarked+cabinKnown+smallFamily+child+fareShared+alone+Age,data=train, mtry=3,importance=T)
> varImpPlot(rf)
Alone and Embarked seems to be not so efficient features. Since main objective of this blog is seeing how generated features are performing, let's keep them.
We will predict the Survived passengers by using 'Neural Networks'. Neural networks accepts variables that are numeric. Furthermore it needs to be in matrix format, not data frame. Model.matrix command does the both.
> matrix.train <- model.matrix(~Survived+Pclass+Sex+Age+Embarked+cabinKnown+large_family+child+fareShared+alone,data=train)
> matrix.train <- matrix.train[,-1]
Neural networks use 'squashing functions' for prediction. Squashing functions map the whole real axis into a finite interval. Famous example for squashing function is sigmoid function, intervals are between zero and one. So, the output of the function is also between zero and one. Think like logistic regression. If we scale our variables between zero and one, neural networks will work more efficiently for this reason. Scaling is also necessary for different scales. In our data set, Age and Fare are something different. We need to scale them.
> maxs = apply(matrix.train,2,max)
> mins = apply(matrix.train,2,min)
> scaled.train <- as.data.frame(scale(matrix.train,center=mins,scale=maxs-mins))
> matrix.test <- model.matrix(~ Pclass+Sex+Age+Embarked+cabinKnown+large_family+child+fareShared+alone,data=test)
> matrix.test <- matrix.test[,-1]
> maxs <- apply(matrix.test,2,max)
> mins <- apply(matrix.test,2,min)
> scaled.test <- as.data.frame(scale(matrix.test,center=mins,scale=maxs-mins))
Now we are ready to train our model.
> nn <- neuralnet(Survived1~Pclass2+Pclass3+Sexmale+EmbarkedS+EmbarkedQ+cabinKnownTRUE+large_familyTRUE+childTRUE+fareShared+aloneTRUE+Age,data=scaled.train,hidden = 4,linear.output = F, act.fct = "tanh")
> pr.nn <- neuralnet::compute(nn,scaled.test)
> x = (pr.nn$net.result > 0.5)*1
"Tanh" is another squashing function that is equal to 2*sigmoid(x) - 1. Hidden is the number of units in the hidden layer. If we code plot(nn) we can see the structure.
> plot(nn)
To submit our prediction to kaggle code
> submit <- cbind(test$PassengerId,x)
> submit = data.frame(submit)
> colnames(submit) = c('PassengerId','Survived')
> write.csv(submit,'submit.csv',row.names = F)
and submit! Score will be about 0.72, which is an average score among competitors.
In this blog we saw how to use 'dplyr' language at basic level, ggplot, very basic side of feature engineering and some introduction to machine learning algorithms. This blog is highly inspired from other kernels which can be found on Kaggle like this one. In the next blog, I would like to talk more about neural networks! Stay tuned until next time!














No comments:
Post a Comment